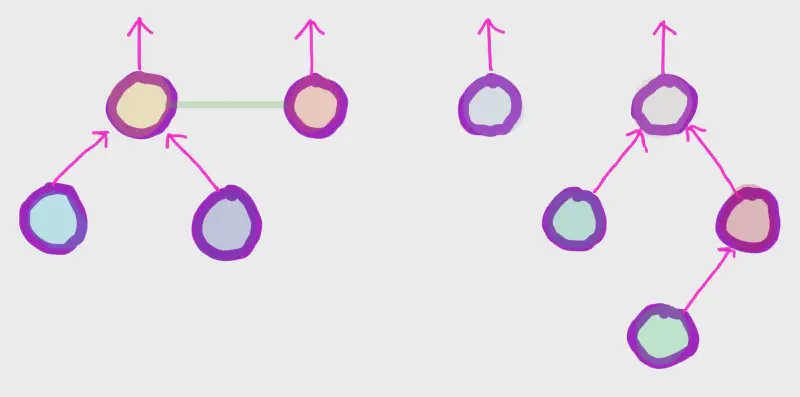
并查集,即不相交集合,用数据结构中的“森林”表示。主要操作有初始化、查询、合并。
初始化
每个元素都建立一个只含自己的集合,每个元素都是自己所在集合的代表,把每个元素的父结点设为自己。
查询
一个元素所在有根树的根结点,就是这个集合的代表元素。
合并
合并两个元素所在的集合,首先找到这两个集合的代表元素,然后其中一个作为另一个的父亲就可以了。
按秩合并优化
每次合并时都尽可能让合并后有根树的最大深度不要过深,从而避免出现类似一条链的情况发生。
秩是指结点高度的上界,在按秩合并中,具有较小的秩的根在合并时要指向具有较大秩的根。
用数组 rank 存储每个结点的秩,在合并时判断秩的大小来决定谁作为根结点。
路径压缩优化
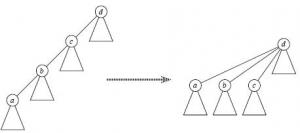
查找的时候,路径压缩优化会将从 a 到 d 路径上所有点都指向有根树的根。这样有根树的高度可以尽可能的降低,下次再操作就更省时了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#include <iostream>
using namespace std;
class DisjointSet {
private:
int *father, *rank;
public:
DisjointSet(int size) {
//初始化
father = new int[size];
rank = new int[size];
for (int i = 0; i < size; ++i) {
father[i] = i;
rank[i] = 0;
}
}
~DisjointSet() {
delete[] father;
delete[] rank;
}
//查询
int find_set(int node) {
if (father[node] != node) {
father[node] = find_set(father[node]);
}
return father[node];
}
//合并
bool merge(int node1, int node2) {
int ancestor1 = find_set(node1);
int ancestor2 = find_set(node2);
if (ancestor1 != ancestor2) {
if (rank[ancestor1] > rank[ancestor2]) {
swap(ancestor1, ancestor2);
}
father[ancestor1] = ancestor2;
rank[ancestor2] = max(rank[ancestor1] + 1, rank[ancestor2]);
return true;
}
return false;
}
};
int main() {
DisjointSet dsu(100);
int m, x, y;
cin >> m;
for (int i = 0; i < m; ++i) {
cin >> x >> y;
bool ans = dsu.merge(x, y);
if (ans) {
cout << "success" << endl;
}
else {
cout << "failed" << endl;
}
}
return 0;
}
|
在数据结构里,森林是由若干棵互不相交的树组成的。
森林有两种遍历方法,分别是先序遍历和后序遍历。请注意,森林是没有和树的中序遍历对应的遍历方法的。
因为中序遍历只存在于二叉树中,而森林中的树都是一般树,无法区分左右孩子,自然也就无法进行中序遍历了。